仕事で東大や京大卒の人達と一緒に仕事をする機会が何度かありましたが、彼ら（彼女ら）と一緒に仕事をして、初めて知った概念があります。
それが、仮説思考です。
この仮説思考とは、仮の結論を立ててから検証を進めることで、効率的かつスピーディーに問題を解決していく思考法のことです。
世間では時に「高学歴の人は仕事ができない、使えない」と揶揄されることもありますが、彼らはむしろ仮説思考を使いこなして、複雑な課題に対しても柔軟に対応して成果を上げていました。
そして彼ら（彼女ら）は、こんなこと言っていました──。
東大にゃん仮説思考は、算数（数学）を通じて身につけることができます。
逆に算数（数学）が苦手な子は、仮説を立てて問題に向き合う習慣が不足しているんじゃないかな？
もし、「算数の小テストは満点なのに、模試になるとまったく点が取れない」という悩みを抱えている場合、仮説を立てて考える習慣を身につけることで、偏差値アップにつながると思います。
算数は解き方を覚えてもできるようにはならない
わたしは、今まで算数（数学）は「解き方を覚えればできるはず──。」と考えていました。
しかし実際はそうではなく、中学受験レベルになると、公式や手順の暗記を問うのではなく、与えられた条件の関係を捉え、仮説を立てて検証する力を試す科目であることに気づきました。
そのため、努力の方向が「解き方の暗記」に偏るほど、応用問題の前で思考が止まりやすくなります。
たとえば「つるかめ算」を親が先回りして教えると、子どもは「このタイプはつるかめ算で解ける」とだけ覚え、別の題材に変わると応用が効かなくなります。
つまり、小テストでは「みかんと箱」で面積図を使って解けたとしても、模試で「仕事と日数」に置き換わった途端に手が止まるのは、問題の題材と解法を一対一に結びつけて記憶しているからだと思われます。
ただ、基礎を軽視してよいわけではなく、計算（公式）や頻出パターンの暗記は、思考を前に進めるためにも必要です。
特に、分数と小数の変換、円周率の計算などは、自動化（暗記）しているほど、脳は計算の負荷から解放され、問題の骨格を捉えることに集中できると思います。
ととにゃん“暗記”と“思考”は対立ではなく両輪であり、「計算の自動化（暗記）が仮説思考の精度やスピードを上げる」ということです。
仮説思考力を伸ばすトレーニング方法
仮説思考力を伸ばすには、どうすればいいのかを一緒に仕事をしていた東大卒の人に尋ねたところ、
東大にゃん最初は、数独パズルから入るのがオススメですよ。
と教えてくれました。
仮説思考の基礎を作る「数独パズル」
数独パズル（ナンプレ）は、 数字を使った論理パズル で、論理的な推理力を鍛えるのに最適な学習法だと思います。
数独パズルでは、１～９の数字を一定のルールに従って配置する下記のような問題です。
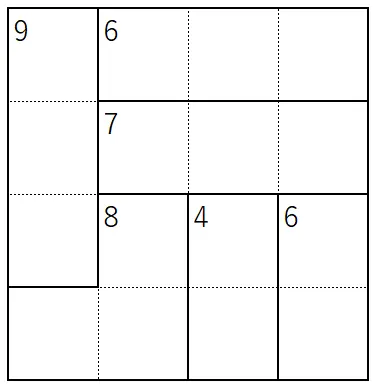
- 図のマスに１～４までの数字を１つずつ入れます
- どの列（たて、よことも）にも１～４の数字が１つずつ入ります
- ブロックの中の数字は、太線でかこまらたブロックに入る数の和（たしたもの）になります
この問題だと、左側にある９を作るには、４＋３＋２を作る必要があるので、左下には必ず１が入ることがわかります。
そして、４を作るには、３＋１の組み合わせしかないので、必ず下記のようになります。
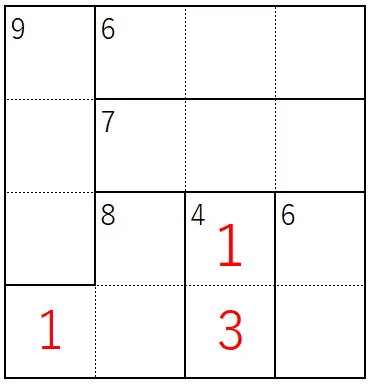
このように、筋道（仮説）を立てながら考える力を養うことができます。
また、計算自体は単純なので、取り組みやすい（集中しやすい）のも魅力の１つです。
ポチップ
算数のセンスも磨く「合格パズル」
なお、中学受験を目指す場合、「数独パズル」だけでは少し簡単すぎるので、本格的に仮説思考の力を伸ばすのであれば、宮本哲也さんの『合格パズル』シリーズがオススメです。
ポチップ
東大にゃん「合格パズル」は、算数のセンスを磨くのにも最適な教材だと思います。
ととにゃんなお、合格パズルでは下記のような問題が出題されています。
ととにゃん『合格パズル』は１～４まで出版されていますが、難易度に差はないため、どの巻から購入しても問題ありません。
合格パズルに取り組む際の注意点
なお、『合格パズル』を進めるうえで、東大卒の方から教えていただいた大切な注意点が１つあります。
それは、問題が解けなくても、絶対に答えを教えないことです。
日を改めて繰り返し挑戦することで、ある日、解法を思いつく瞬間がでてくるので、絶対に答えを教えずに考え抜くようにアドバイスをもらいました。
実際にわが家の子どもは、この『合格パズル』に取り組んでいたこともあってか、小テストでは教室内で１番になることはありませんでしたが、模試では教室内で１番になることがありました。
ととにゃんこの傾向は中学以降も同様で、定期テストより全国模試の方が学内順位が良いことが多いです。
学習塾では「仮説思考」は身につけにくい
大人数の集団塾でも少人数制の個別指導でも、多くの塾では講師不足への対応として授業の均質化や映像化が進み、マニュアルに沿った指導が中心になっていると感じます。
これは一定の品質を保てる反面、どうしても「解法の暗記」に偏りやすいという副作用も生み出しています。
特に下位クラスでは「とにかく解けるようにする」即効性が優先され、仮説を立てて考えるプロセスが省かれがちだと考えます。
そのため、「塾に任せれば安心」と考えるのではなく、「塾で得られない部分を家庭で補う」という発想に切り替えるといいと思います。
なお、塾で得られない部分を補うというのは、解法を理解させるということではなく、「合格パズル」のような教材に取り組み、親子で一緒に考える体験を通して、思考の土台を作ることです。
ととにゃんわが家の場合は、小学５年生以降、「合格パズル」のような問題を子どもが作り、わたしがそれを解かなければいけないという拷問のような時間に変わりました──。
何はともあれ、仮説思考を伸ばす“きっかけ”として「合格パズル」はおすすめです。
ポチップ
コメント