【保存版】中学受験で覚えておきたい算数の暗記事項5選｜無料プリント付き

わが家の子どもが中学受験をする前は、計算が速い人は、そろばんを習っていたり、特別な才能があるのだと思っていました。

でも、それは違いました──。

計算が速い人は、「無駄な計算をそもそもしていない」ということに気付きました。

たとえば、こんな計算を10秒以内にできるでしょうか？

0.625 × 0.4 ＝

もし計算できないようであれば、このページで紹介している計算結果を覚えるだけでも、計算のスピードや正確さが大きく向上すると思います。

覚えるべき小数と分数の変換

小数は分数に変換することで、計算が速くなります。

下記の小数は頻繁に登場するので、すべて暗記してしまいましょう。

少数	分数
0.5	\( \frac{1}{2} \)
0.25	\( \frac{1}{4} \)
0.75	\( \frac{3}{4} \)
0.2	\( \frac{1}{5} \)
0.4	\( \frac{2}{5} \)
0.6	\( \frac{3}{5} \)
0.8	\( \frac{4}{5} \)
0.125	\( \frac{1}{8} \)
0.375	\( \frac{3}{8} \)
0.625	\( \frac{5}{8} \)
0.875	\( \frac{7}{8} \)
0.0625	\( \frac{1}{16} \)
0.05	\( \frac{1}{20} \)
0.04	\( \frac{1}{25} \)
0.008	\( \frac{1}{125} \)

試しに、\( 5.625 \times 16 \) を計算してみます。

まず、\( 5.625 = 5\frac{5}{8} = \frac{45}{8} \) のように分数に変換します。

よって、\( \frac{45}{8} \times 16 \) となり、分子と分母を約分します。

$$ \frac{45 \times \cancel{16}^{2}}{\cancel{8}} = 45 \times 2 = 90 $$

答えは、90 となります。

このように小数が入った計算式は、分数に変換することで計算しやすくなることがあります。

3.14（円周率）を使った計算

3.14（円周率）を使った計算の暗記は、必須事項です。

これを暗記することで、計算ミスが少なくなるだけではなく、普段の勉強でもよりたくさんの問題数を解けるようになります。

計算式	計算結果
2 × 3.14	6.28
3 × 3.14	9.42
4 × 3.14	12.56
5 × 3.14	15.70
6 × 3.14	18.84
8 × 3.14	25.12
9 × 3.14	28.26
12 × 3.14	37.68
15 × 3.14	47.10
16 × 3.14	50.24
25 × 3.14	78.50
36 × 3.14	113.04

平方数を使った計算

平方数は面積の問題を解く際に頻繁にでてくる数値なので、この計算結果も暗記してしまいましょう。

計算式	計算結果
11×11	121
12×12	144
13×13	169
14×14	196
15×15	225
16×16	256
17×17	289
18×18	324
19×19	361

できれば、平方数だけでなく、11〜19の段（1の位とのかけ算）も、あわせて覚えておくといいと思います。

立方数を使った計算

立方数とは、同じ整数を３回かけあわせてできる数のことです。

体積を計算する際に必要になるので、この計算結果も暗記してしまいましょう。

計算式	計算結果
2×2×2	8
3×3×3	27
4×4×4	64
5×5×5	125
6×6×6	216
7×7×7	343
8×8×8	512
9×9×9	729
10×10×10	1000

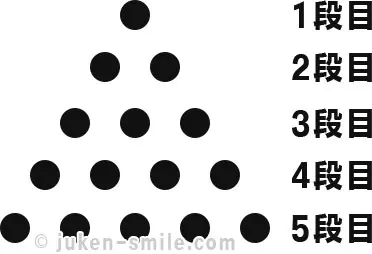
三角数

三角数とは、1つずつ増える自然数の和として表される数で、図で表すと正三角形の点の形になる数のことです。

n番目	三角数（Tn）
3番目	6
4番目	10
5番目	15
6番目	21
7番目	28
8番目	36
9番目	45
10番目	55
11番目	66
12番目	78
13番目	91
14番目	105
15番目	120

この三角数の公式を図解すると次のよう説明することができます。

黒いご石を図のように並べていくとき、12段目まで並べるには、全部で何個のご石が必要になりますか？

三角数は小学校で習う範囲内で出題できるため、適性検査でも出題されやすいので暗記しておきましょう。

まとめ

この記事では、暗記することで計算が速くなる数や公式を紹介しました。

この他にも、多角形の内角の和や葉型の面積など、覚えておくと計算がスムーズになるものはいくつかあります。

私立中学を本命にされているなら、そういった知識もあわせて覚えておくと安心です。

わが家では、こうした算数の暗記事項をトイレに貼って覚えていましたが、単語帳にまとめて持ち歩くのもおすすめですよ。