わが家の子どもは、小学1、2年生の時に近所の学童のような教室に週1回通っていました。
ある日、その教室の先生からこんな言葉をかけられました。
困ったにゃん(子どものこと)は、数字に強いから「算数検定」を受けてみたら?
そこで、実際に「算数検定 10級」の問題集を購入してみると、思った以上に難しく、それでいて問題が工夫されていて面白い──と感じました。
そのため、算数検定の問題を参考にして、オリジナル問題を作り、子どもに解かせたところ、楽しんで取り組んだこともあって、毎年、算数検定を受けていました。

わが家の子どもは「ドラゴンクエスト」が好きだったこともあって、ドラクエの絵を描いて問題にしたら食いついてきました。
この問題の解答は下側にあるよ。
算数検定とは?
算数検定の正式名称は「実用数学技能検定」で、公益財団法人・日本数学検定協会が主催する全国規模の検定試験になります。
各級のレベルと出題範囲
算数領域は「算数検定」、数学領域は「数学検定」と呼ばれ、級ごとに体系的に区分されているため、学年や習熟度に応じて段階的に挑戦できます。
幼児向けの「かず・かたち検定」もあるよ。
| 級 | 対象学年の目安 | 出題範囲 |
|---|---|---|
| 11級 | 小学1年程度 | たし算・ひき算、大小比較、時計の読み方 |
| 10級 | 小学2年程度 | 九九(かけ算)、簡単なわり算、長さ・かさ・時刻 |
| 9級 | 小学3年程度 | 3桁×2桁のかけ算、あまりのあるわり算、円・三角形の基礎 |
| 8級 | 小学4年程度 | 分数・小数の計算、面積、直方体や立方体の体積の基礎 |
| 7級 | 小学5年程度 | 約数・倍数、平均、割合、速さ、円周率 |
| 6級 | 小学6年程度 | 比例・反比例、角度、体積・容積、図形の性質 |
| 5級 | 中学1年程度 | 正負の数、文字式、方程式、一次関数、立体の表面積 |
| 4級 | 中学2年程度 | 連立方程式、一次関数の応用、合同・相似、確率 |
| 3級 | 中学3年程度 | 二次方程式、平方根、ピタゴラスの定理、円周角の定理 |
| 準2級 | 高校基礎(高1程度) | 二次関数、三平方の定理の応用、確率分布、標本調査 |
| 2級 | 高校中級(高2程度) | 指数・対数、三角比、数列、確率と統計 |
| 準1級 | 高校上級(高3程度) | 微分・積分の基礎、ベクトル、複素数平面 |
| 1級 | 大学程度 | 数学全般(大学入試~基礎数学レベル)、総合的な応用力 |
なお、5級以上は「一次試験(計算技能検定)」と「二次試験(数理技能検定)」の二部構成になっていて、一次では計算力、二次では思考力・応用力を問う問題が出題されます。
受検の流れと申し込み方法
2025年7月以降、算数検定の申し込み方法は、インターネットまたはLINE公式アカウントに一本化されました。
従来の郵送による受付は廃止されていますので、ご注意ください。
ちなみに個人受検には、主要都市で年3回実施される「A日程」と、提携団体で随時開催される「B日程」があります。
検定料の目安
- 算数検定(6~11級)・・・2,700~3,200円
- 数学検定(1~5級)・・・4,300~8,500円
なお、3級以上の受検には顔写真付きの受検証が必要ですが、4級以下では不要です。
中学受験に向けて感じた算数検定のメリット
算数検定は、学習指導要領に準拠していることもあり、「基礎がどこまで身についているか」を確認するのに最適な試験(問題)だと思います。
今振り返ると、算数検定での基礎固めがあったからこそ、中学受験(適性検査)の算数にも抵抗なく取り組めたのかもしれません──。
また、検定後には単元ごとの正答率や弱点が明確に示された「個別成績表」が発行されるうえ、合格証を手にすることで達成感を得られることもできます。
「全国統一小学生テスト」との比較
「全国統一小学生テスト」は、全国順位や偏差値といった客観的な数値を把握することを主な目的としています。
その性質上、平均点が高くなりすぎないよう調整されており、出題には中学受験を意識した応用問題や難問も含まれるため、全問正解は至難の業です。
一方、算数検定は基礎力の定着度を測る実用的な検定であり、しっかりと学習すれば満点を狙うことも可能です。
このように両者は役割が異なっています。
まとめ
わが家の経験からも、算数検定で積み重ねた学びは中学受験(中学受検)にも役立ちました。
算数が好きなお子さんはもちろん、苦手意識のある子にとっても「学ぶ力」と「考える力」、そして目標達成する力を育む第一歩になると思います。
ちなみに、オリジナル問題は「算数検定 10級」にあった問題を参考にしたと思います。
オリジナル問題の解答例
問題文を再掲します。
スライムとドラキー、キングスライムの経験値はあわせて、31EXP1です。
スライムは、キングスライムより、7EXP少ないそうです。
ドラキーは、キングスライムより、4EXP少ないそうです。
スライムの経験値は、いくつでしょうか?
- EXPは経験値(Experience)の略 ↩︎
スライムの経験値(EXP)を基準とした線分図を描くと下記のようになります。
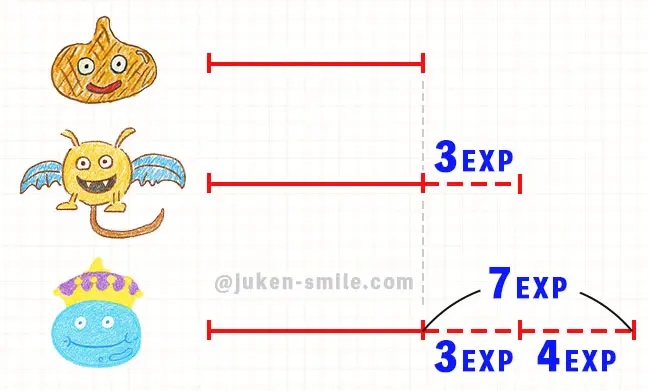

ドラキーの経験値(EXP)は、キングスライムより4EXP少ないので、スライムより、3EXP多いことになります。
続いて、上記の赤い点線部分(3EXP+7EXP)から、経験値の合計の31EXPを引きます。
すると、31ー10=21EXPが、赤い実線部分になります。
この21EXPを、スライムドラキー、キングスライムで分けることになるので、
21÷3=7EXP
が答えになります。













コメント