この問題は、公式(三平方の定理)を使うと一発で解けるんだよ。
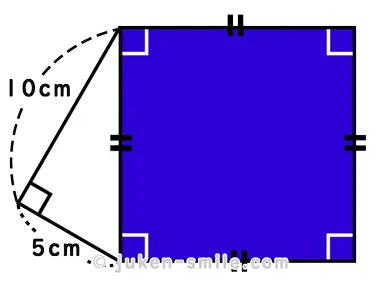

まぁ、この問題は、三平方の定理を使わないと逆にどうやって解くんだ?!
といった感じですが、中学受験の算数では、一般的な学校教育では習わないものの、入試という限った場面で有効な公式(解法)が存在します。
そこで今回は、「この公式、知っておいてよかった!」と、子どもがつぶやいていた公式(解法)をいくつかまとめてみました。
葉っぱの形の面積について
「葉っぱの面積」とは、正方形の中に、向かい合う頂点からそれぞれ半径を1辺とする4分の1の円が描かれ、その2つの円が重なり合う部分にできる図形を指します。
他にも、“レンズ型”、“くちびる”とも呼ばれています。
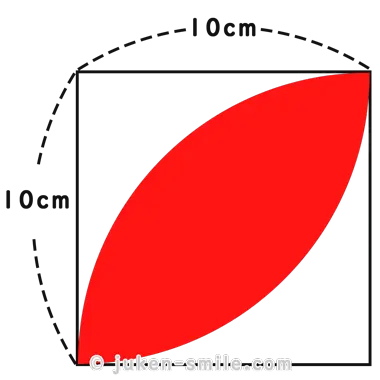

この図形を求める場合、90度のおうぎ形2つ分から、正方形の面積を引く方法があります。
$$ \begin{aligned} 10 \times 10 \times \frac{2}{4} \times 3.14 – 10 \times 10 &= 157 – 100 \\ &= 57\,\text{cm}^2 \end{aligned} $$ただ、このような計算をするまでもなく、この面積を求める公式があります。
それが、「葉っぱの形は正方形の0.57倍」です。
なお、葉っぱの形以外の白い部分は、それぞれ正方形の0.215倍になります。


ヒポクラテスの三日月について
「ヒポクラテスの三日月」とは、直角三角形の各辺を直径とする半円を描いたときにできる、三日月形(ルーン)の面積が、もとの直角三角形の面積と等しくなるという、古代ギリシャの数学者ヒポクラテスに由来する有名な幾何学的原理です。
ちょっと、何言っているのかわからない・・・。
図で説明すると、赤く着色されている部分(三日月部分)と、青く着色されている部分(直角三角形)の面積が等しくなるというのが、ヒポクラテスの三日月です。


出題例です。
底辺5cm、高さ12cm、斜辺13cmの直角三角形の各辺を直径とする半円を描いた図形において、赤く着色されている部分(三日月形)の面積を求めなさい。ただし、円周率は3.14とする。


本来であれば、
((直径5cmの)半円の面積 + (直径12cmの)半円の面積 + 直角三角形の面積) - (直径13cmの)半円の面積
の計算をする必要がありますが、ヒポクラテスの三日月の公式(原理)を使えば、直角三角形の計算をするだけで答えがでます。
$$ 5 \times 12 \div 2 = 30\,\text{cm}^2 $$台形の蝶々型について
台形に2本の対角線を引くと、内部が4つの三角形に分割されます。
このときの構図が蝶のように見えることから「台形の蝶々型」などと呼ばれ、中学受験では頻出の図形になります。
この「台形の蝶々型」は、台形の上底と下底が、a:bであるとき、次のような公式が成り立ちます。


たとえば、次のような形で出題されます。
三角形AEDと三角形ABEと三角形EBCの面積比を求めよ
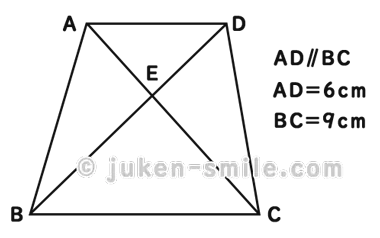

AD=6cm、BC=9cmのため、相似比は2:3より、次のように計算できます。
$$ \begin{aligned} &\triangle AED\ (a^2)、\quad \triangle AEB\ (ab)、\quad \triangle EBC\ (b^2) \\ &\text{となるので面積比は、 } 4 : 6 : 9 \end{aligned} $$断頭三角柱について
断頭三角柱(だんとうさんかくちゅう|切頭三角柱)とは、三角柱の上または下を斜めに切った立体になります。
こちらも、中学受験では頻出の図形となり、以下の様な公式があります。
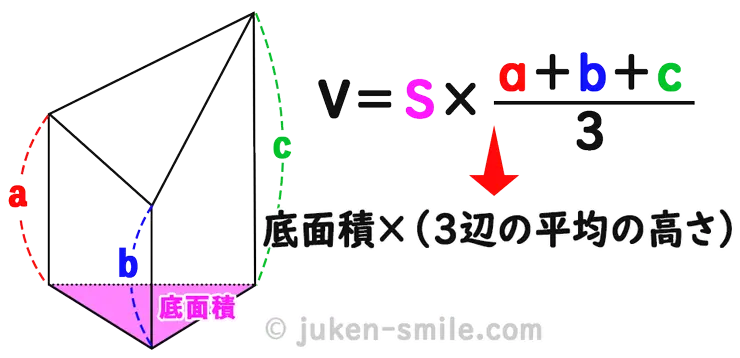

出題例です。
三角柱を1つの平面で切断した下記の立体の体積を求めよ
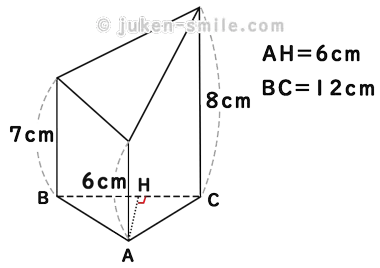

この問題は、元の三角柱の体積から、切り取った四角錐(しかくすい)の体積を引くことで求めることが出来ますが、四角錐の面積を計算するのが面倒です。
そのため、底面積×(3辺の平均の高さ)の公式を使うと、このように計算できます。
$$ \begin{aligned} V &= \left( \frac{12 \times 6}{2} \right) \times \frac{6 + 7 + 8}{3} \\ &= 36 \times 7 \\ &= 252\,\text{cm}^3 \end{aligned} $$なお、この問題は応用として、切断する平面を2か所に増やすなど、さまざまなバリエーションがあります。
まとめ
他にも、中学受験で覚えておくと役に立つ公式はいくつかあると思いますが、図形問題が苦手なわが子が「これは役に立った」と言っていたものを集めてみました。
なお、鶴亀算・流水算・和差算といった特殊算については、表や線分図、面積図などで解くらしく、公式として意識したことはないらしい──です。
基本的には、公式に頼るのではなく、考え方の本質を理解することが大切だと思います。
ただ、「裏技」的な公式が、子どものやる気を引き出すこともあるので、使うかどうかは別として、知っておくとよいのではないでしょうか。












コメント